행렬곱으로 신경망 계산(입력계층 은닉계층간)

우리가 앞에서 신경망을 만들어보고 각 계층간 가중치를 임의로 부여하여 계산을 했었습니다.

그 계산을 이번엔 행렬곱을 통해 해보겠습니다.

앞애서 아래의 이미지로 한번 해봤었죠?

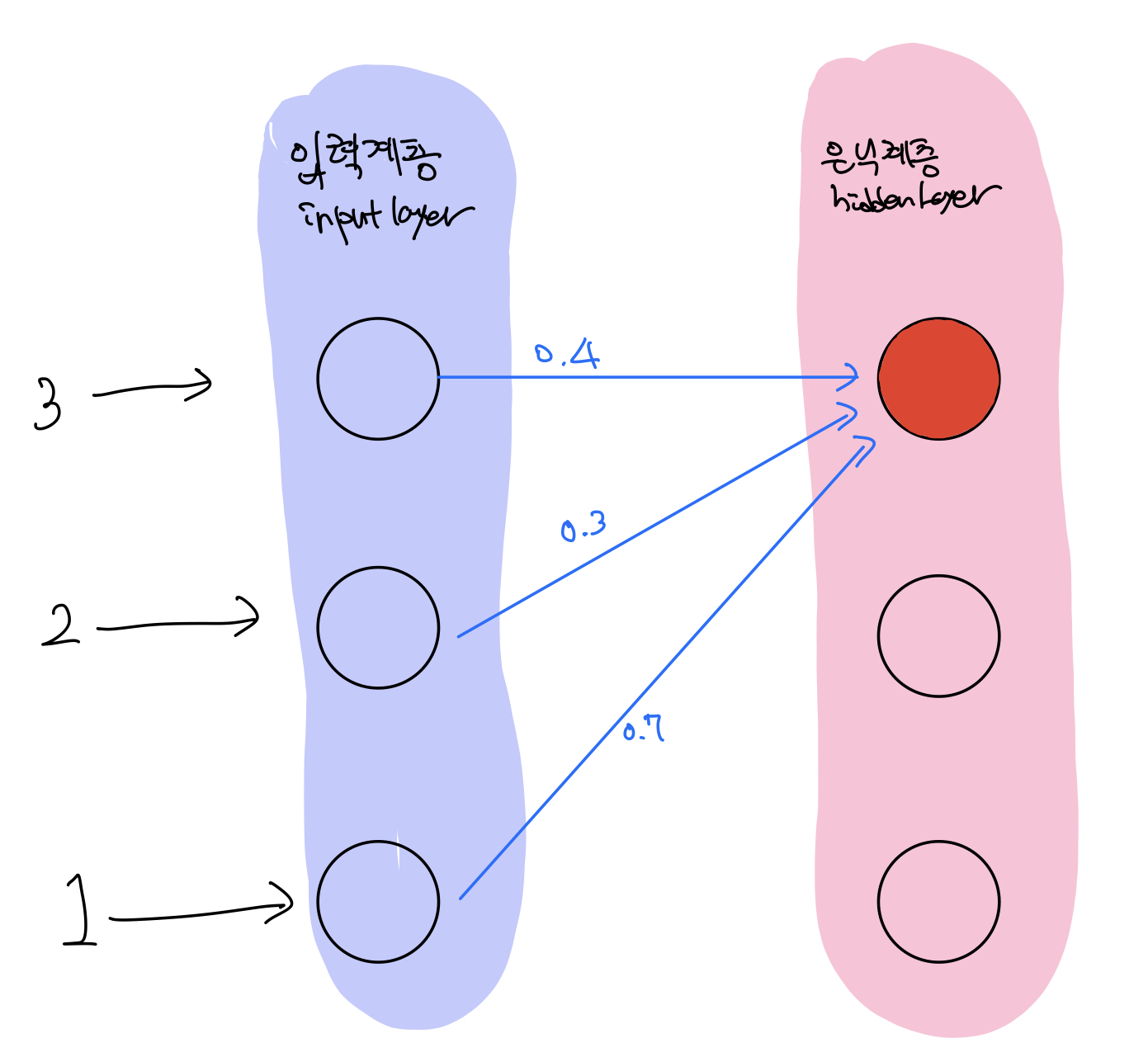
입력이 각 노드에 3,2,1 들어가고 가중치는 각 0.4, 0.3, 0.7이었습니다.

그래서 행렬곱을 하기위해 다음과 같이 표현을 했습니다.

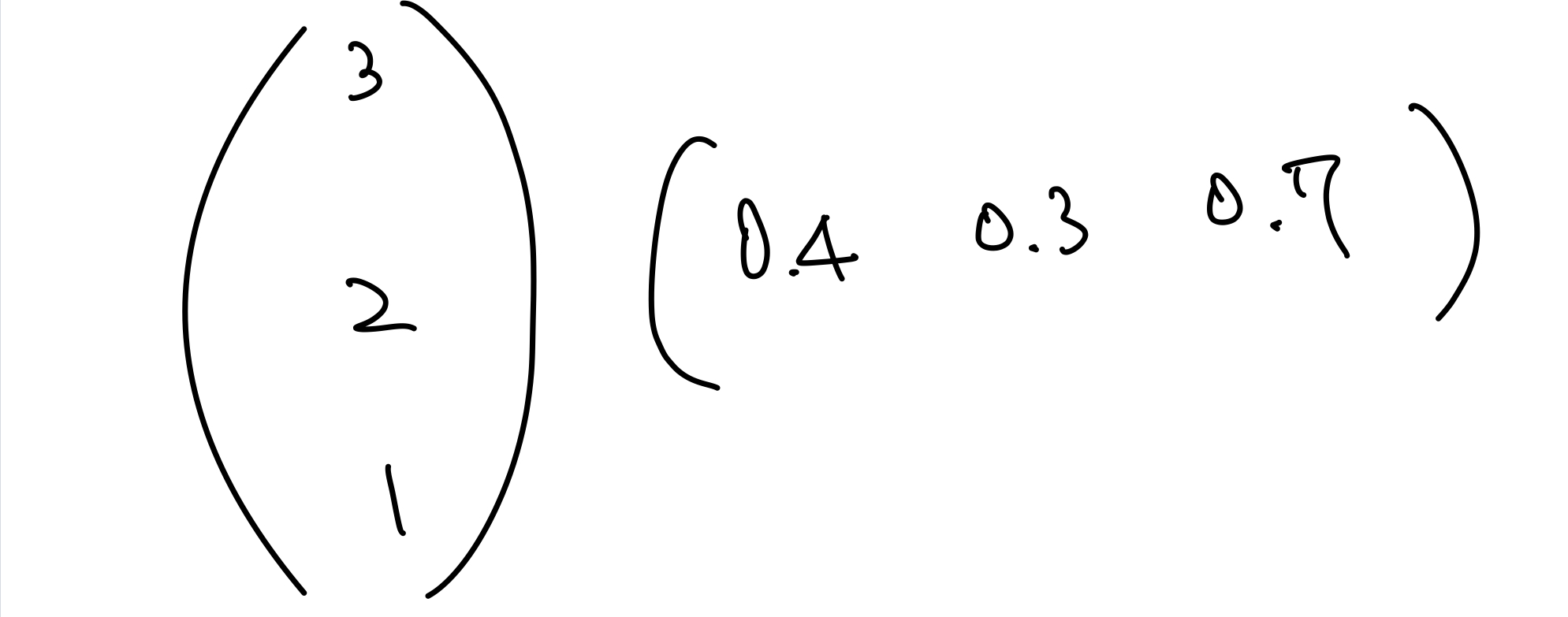
즉 다음 계층을 목표로 가중치를 가로로 나란히 작성했습니다.

그럼 은닉계층의 두번째 노드도 적용해볼게요.

은닉계층의 두번째 노드에는 다음과 같이 가중치를 적용했었죠?

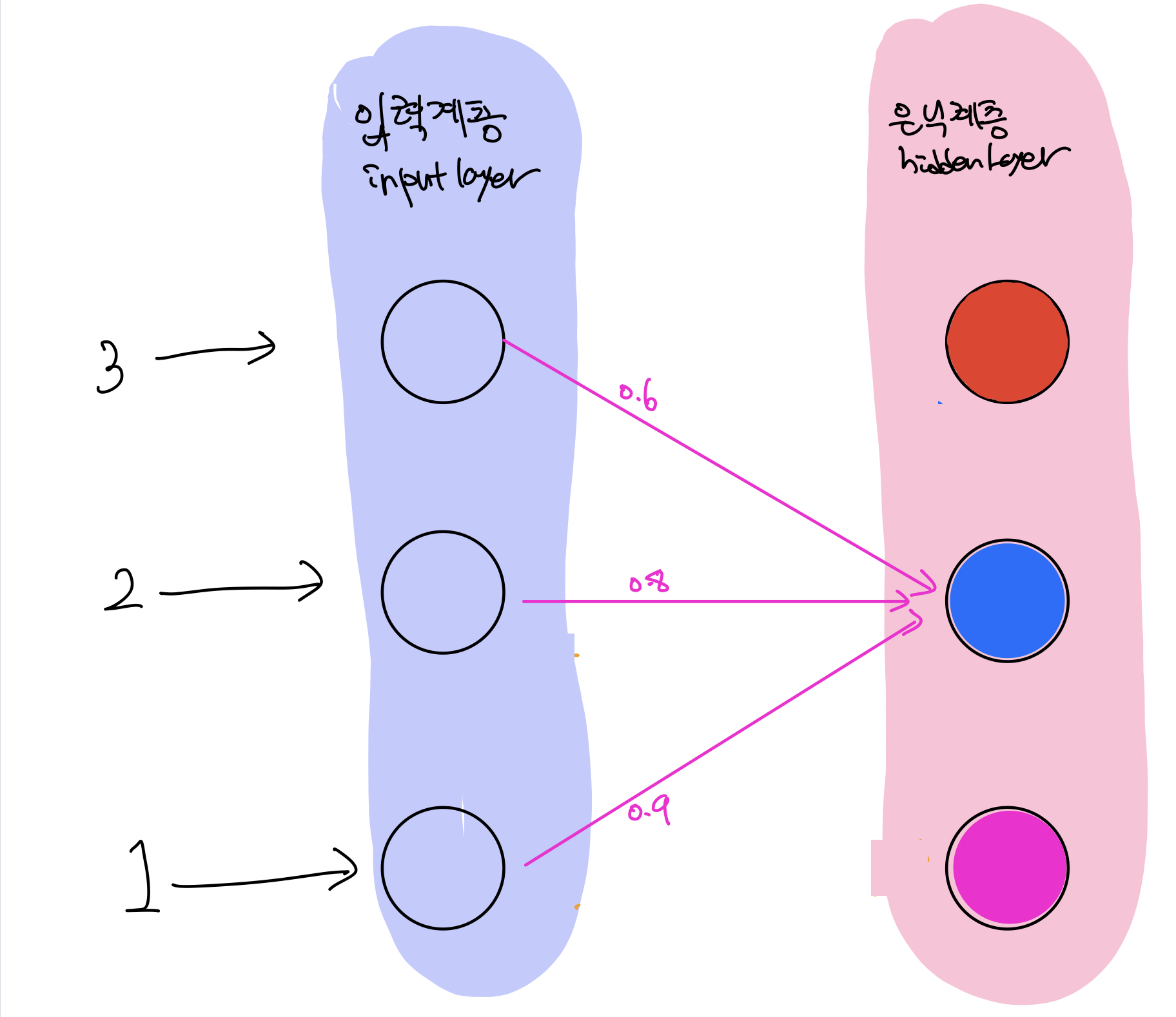
즉 0.6, 0.8, 0.9

그럼 행렬에 그대로 0.6, 0.8, 0.9를 추가합니다.

그럼 행렬식은 다음과 같습니다.

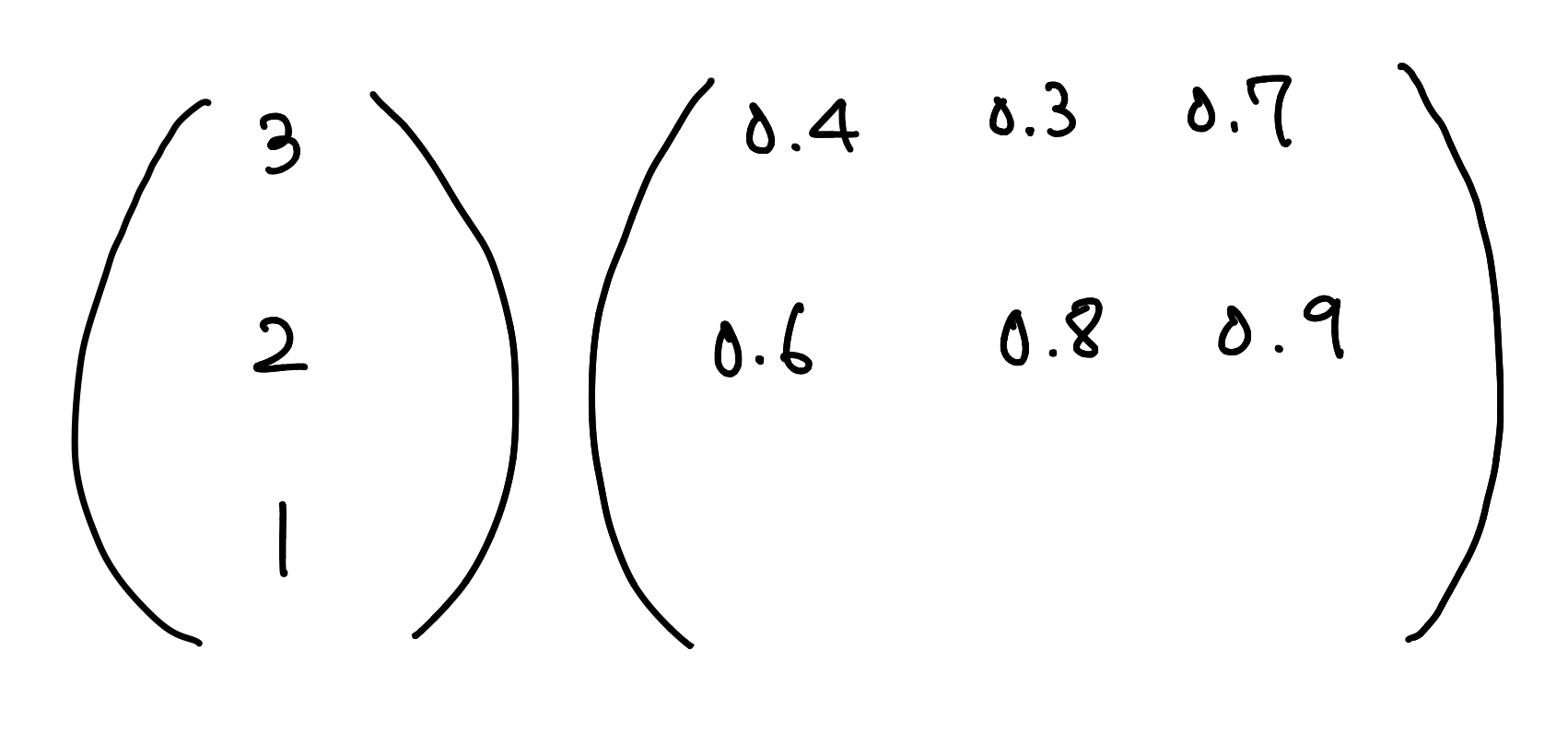
자 그럼 이번에는 은닉계층의 세번째 노드와 연결된 가중치입니다.

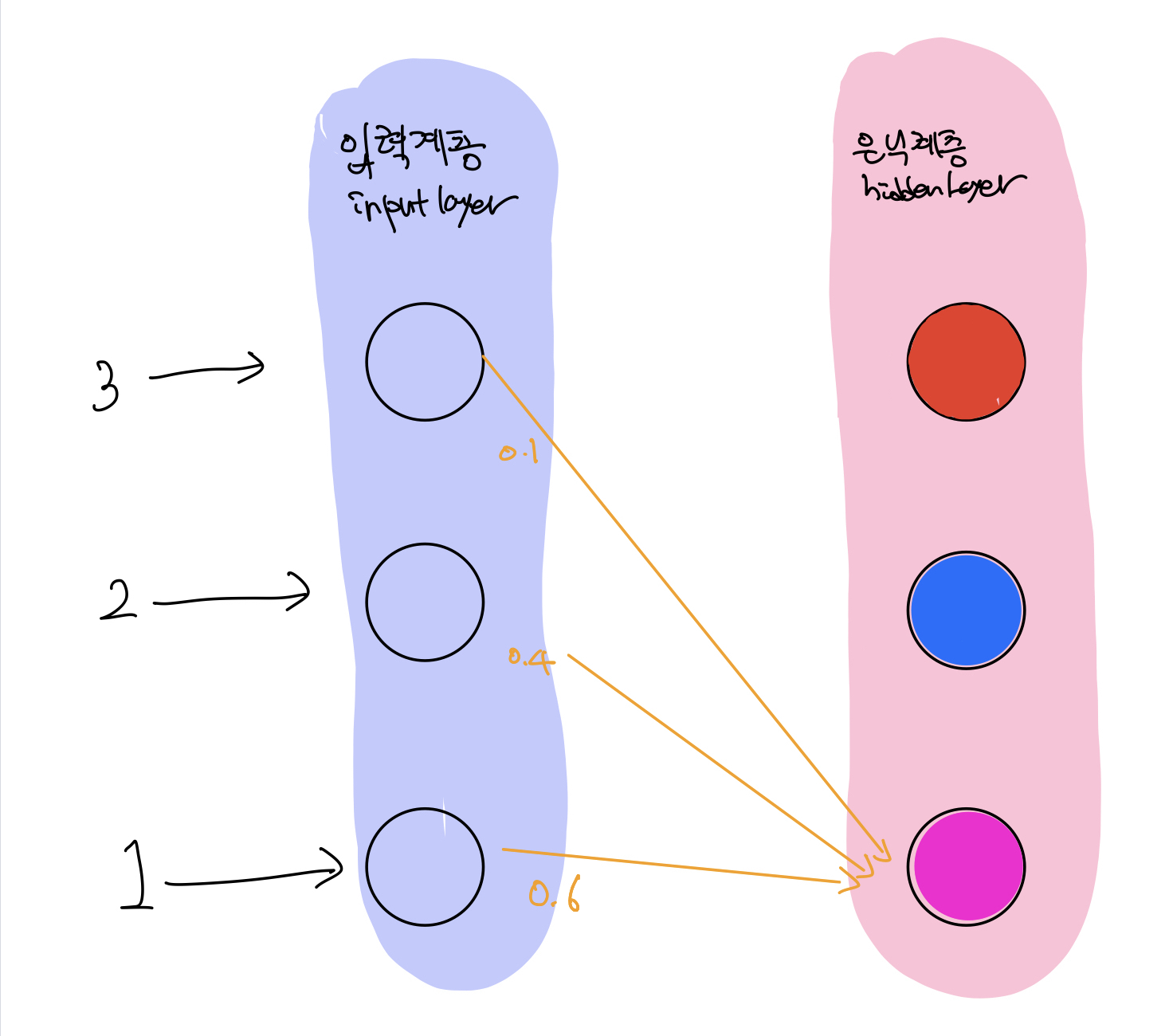
0.1, 0.4, 0.6입니다.

그럼 행렬식은 다음과 같습니다.

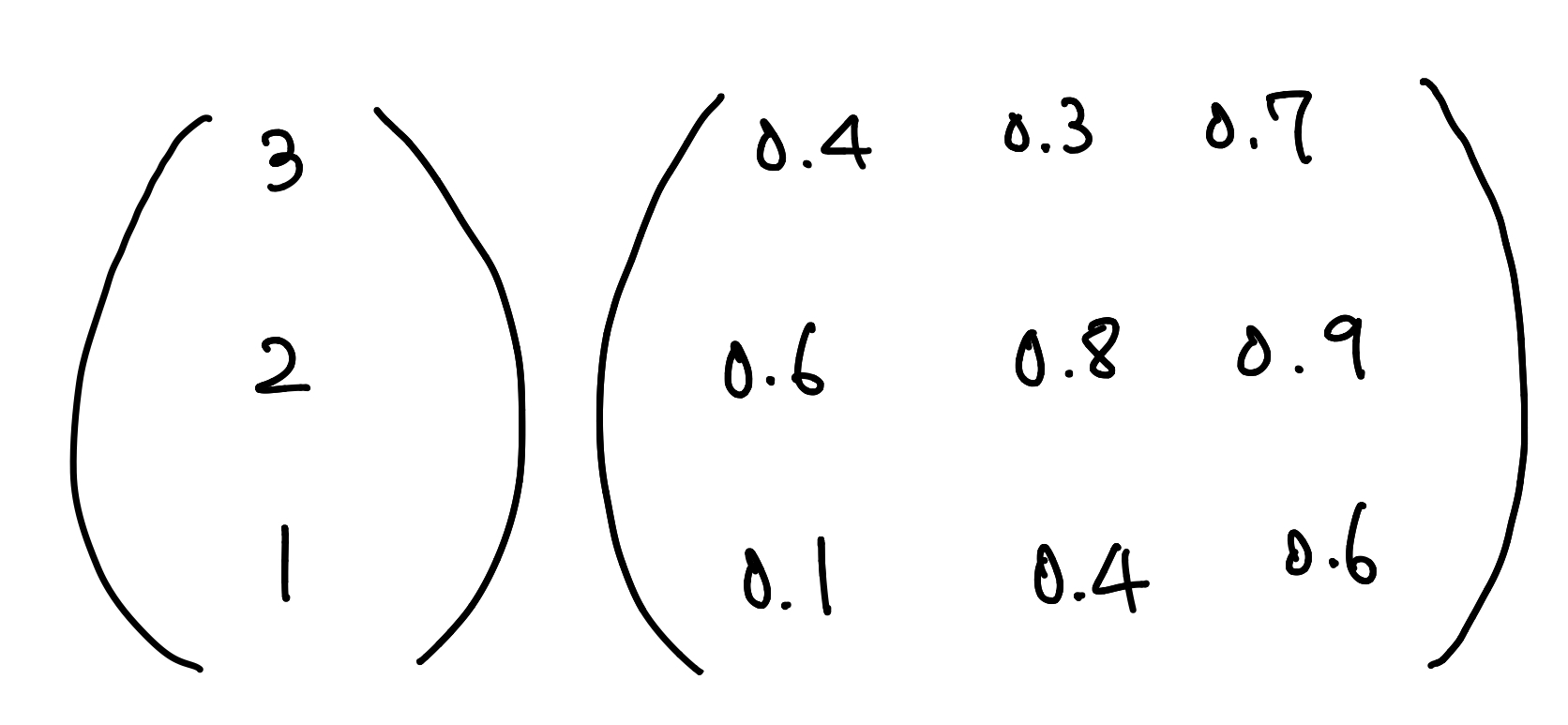
자 그럼 하나씩 풀어볼까요?

먼저 가중치 행렬의 첫번째 행입니다.

그럼으로 표현해본다면 다음과 같죠?

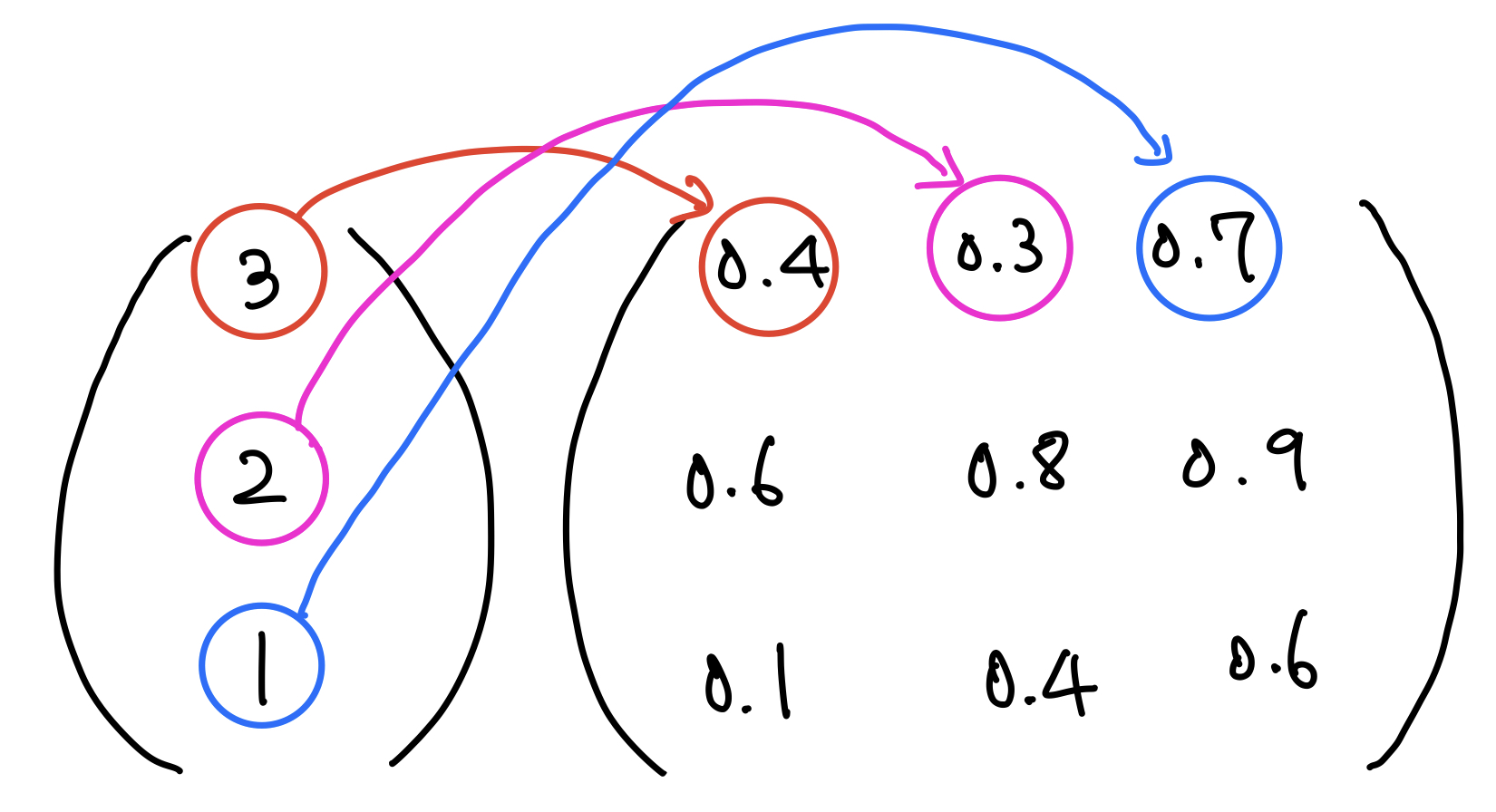
그럼 계산해보면

(3 * 0.4) + (2 * 0.3) + (1 * 0.7) = 1.2 + 0.6 + 0.7 = 2.5

앞의 강좌에서도 한번했지만 2.5가 나왔습니다.

시그모이드 함수 계산은 나중에 한꺼번에 합시다.

자 그럼 다음 계산을

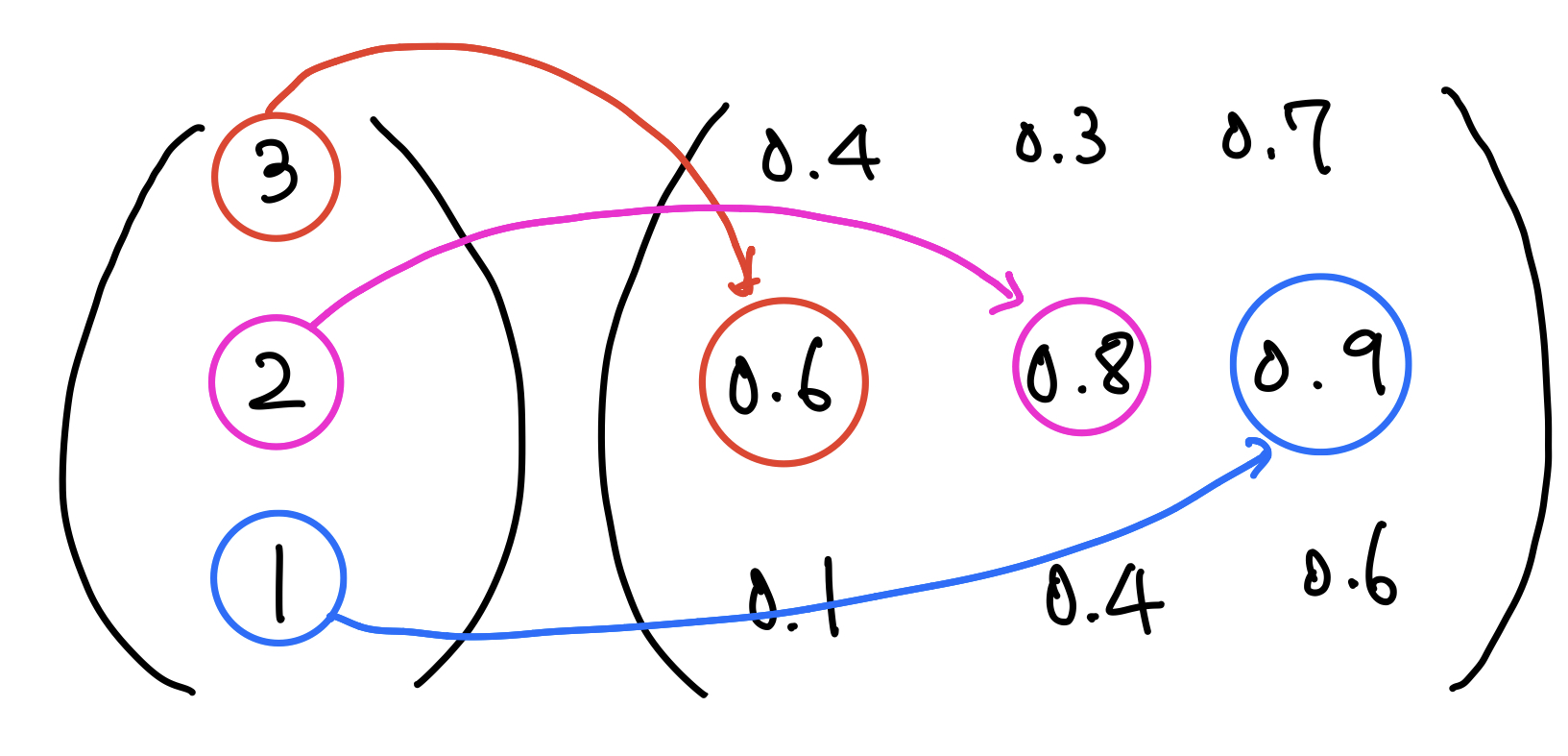
(3 * 0.6) + (2 * 0.8) + (1 * 0.9) = 1.8 + 1.6 + 0.9 = 4.3

당연하지만 같은 값인 4.3이 나왔습니다. 행렬곱으로 굉장히 유용하게 풀 수 있죠. ^^

사실 이 규칙이 어차피 우리가 손이나 계산기로 하나하나 계산하는데 뭐가 좋은지 모를 수 있지만 이 규칙이 있다는것만으로 나중에 프로그래밍하기가 편해지기 때문입니다.

그럼 다음 계산을 하겠습니다.

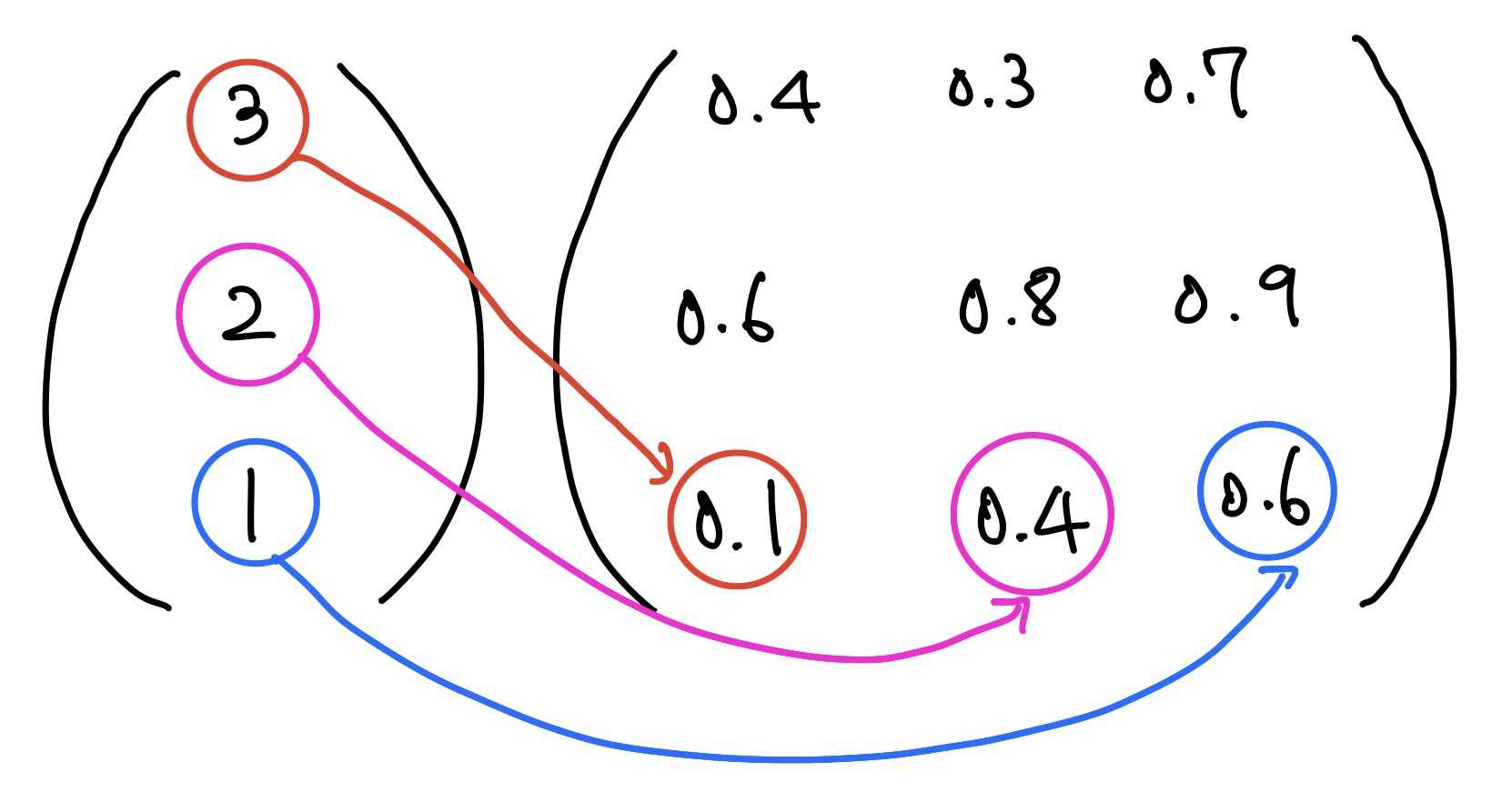
그럼 계산해보면

(3 * 0.1) + (2 * 0.4) + (1 * 0.6) = 0.3 + 0.8 + 0.6 = 1.7

모든 값이 모두 앞에서 우리가 했던것과 동일하게 나왔습니다.

하지만 노드가 받은 값을 출력하려면 시그모이드 함수 처리를 해야하죠.

앞에서 이미 우리는 시그모이드 함수 계산을 했기 때문에 바로 답 적었습니다.

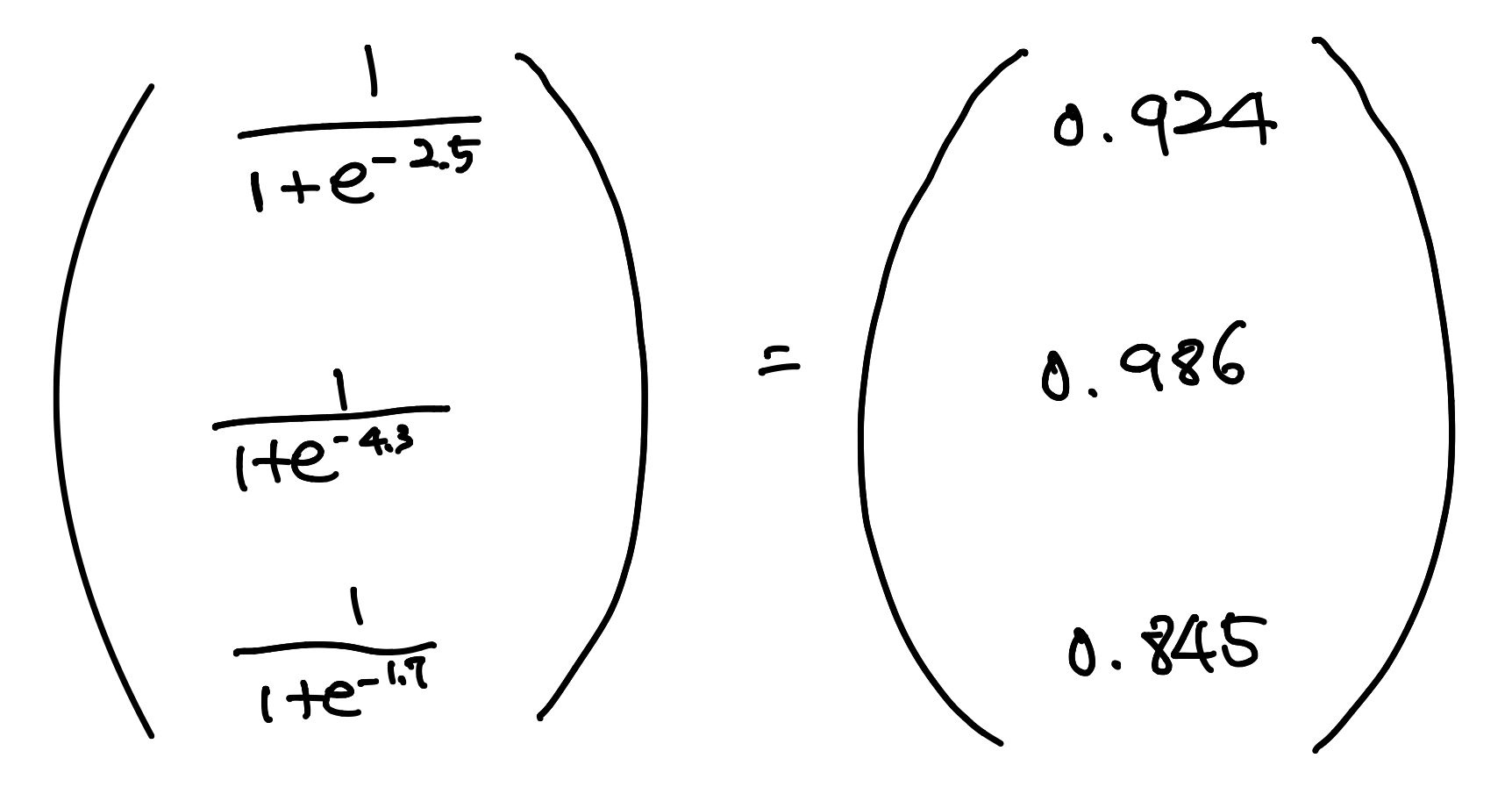
자, 이렇게해서 입력계층이 출력계층에 넘기는 값을 구했습니다.

은닉계층입장에서는 이 값이 입력값이죠? ^^

그럼 이번엔 은닉계층과 출력계층간의 계산을 행렬곱으로 해보겠습니다.

다시 행렬식을 작성하겠습니다.

페이지가 길어지니 다음시간에 이어서 해봅시다. ^^

봐주셔서 감사합니다. 문의 또는 잘못된 설명은 아래의 댓글에 부탁드립니다.
당신의 작은 누름이 저에게는 큰 희망이 됩니다.